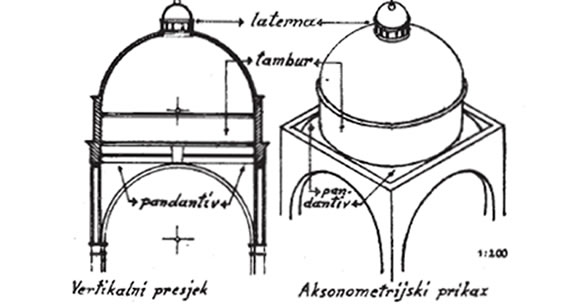
slika 1. Konstruktivni elementi renesansne kupole
Kupole su specijalne vrste svodova nad prostorima kružnog, poligonalnog i pravokutnog (kvadratičnog) tlocrtnog oblika.
Značajnije historijske kupole
Najznačajnija historijska kupola pokriva kružnu površinu rimskog hrama Panteona građenog u II stoljeću n.e. Promjer te kupole (d = 43,60 m) nije premašila ni slijedeća najveća ali 13 stoljeća mlađa (početak renesanse) kupola katedrale u Firenci (d = 41,97 m) ni 14 stoljeća mlađa Mikelanđelova kupola crkve sv. Petra u Rimu (d = 41,40 m).
Kupole nad prostorima kružnog tlocrta
Ove kupole pokazuju u svom vertikalnom presjeku polukružni, a iznimno i segmentni, eliptični ili šiljasti luk (sl. 2.). U manjim i čednijim historijskim zgradama takve su kupole samo konstruktivni elementi, pa se izvana niti ne naglašavaju već pokrivaju krovom.
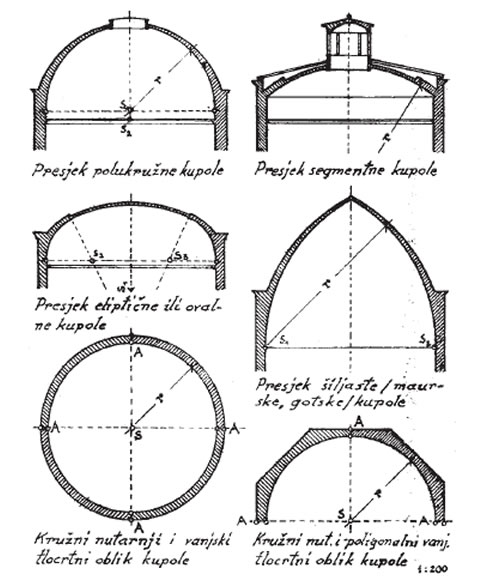
slika 2. Kupole nad prostorima kružnog tlocrtnog oblika
U značajnijim su građevinama kupole ne samo konstruktivni nego i vrlo važni oblikovni i reprezentativni elementi koji zgradu izdižu iznutra i izvana. Često su se nutarnje površine polukružnih kupola rješavale s horizontalnim prstenastim istaknutim rebrima prekidanim takvim meridijalnim rebrima.
Tako su na nutarnjoj površini kupole nastajale kutije ili kazete, pa su zato nazvane kazetirane kupole. Neke su kupole na tjemenu imale kružni otvor ili oko (oculus = okuhis), kao npr. Panteon (d = 9 m). U vrijeme renesanse i baroka podižu se često dvostruke kupole s cilindričnim nastavkom oko okulusa koji se naziva tambur a tambur se opet natkriva manjom kupolom (sl. 3.).
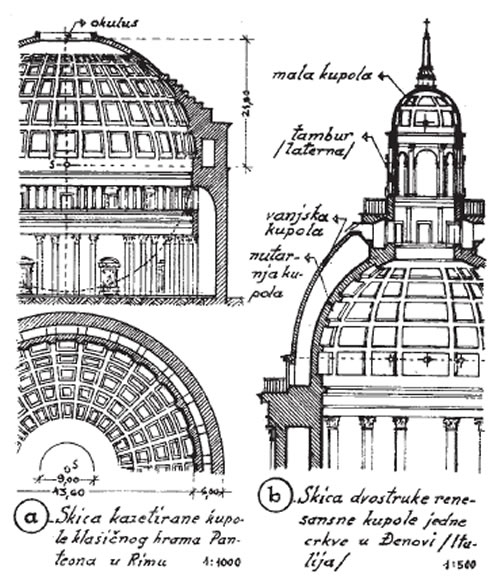
slika 3. Dva karakteristična primjera polukružnih kupola na historijskim zgradama
Kupole nad prostorima poligonalnog tlocrta
Ove se rješavaju kao samostanski svodovi s toliko presječnica koliko je u tlocrtu uglova, a sve se presječnice sastaju u tjemenu kupole (sl. 4.). Umjesto ovakvim kupolama često se spomenuti prostori natkrivaju križnim svodovima, osobito u gotskoj arhitekturi, koja svoje zgrade izvana ističe posebno obrađenim tornjevima.
Kupole nad prostorima kvadratičnog tlocrta
Njih je uvela i često ostvarivala bizantska arhitektura. Jednostavnija je konstrukcija loptasta kupola, kojoj su oba dijagonalna vertikalna presjeka polukružnice. Četiri stranice iznad uporišnih tačaka (U) završavaju se polukružno, i to polukružnim čeonim lukom čiji je promjer jednak tlocrtnoj dužini stranice, ako je prostor određen sa četiri strupa ili pila, a polukružnim obrubom zida, ako je prostor omeđen zidovima.
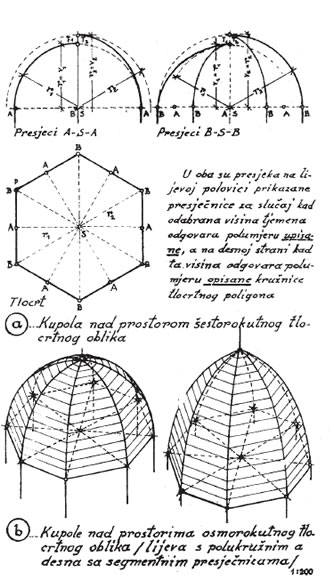
slika 4. Kupole nad prostorima poligonalnog tlocrtnog oblika
Sama kupola određena je spomenutom polukružnicom vidljivom u dijagonalnom presjeku i kružnicom kojoj je promjer jednak dužini dijagonale tlocrtnog kvadrata, pa je to oko kvadrata opisana kružnica (sl. 5.).
Češća je i karakterističnija bizantska kupola. Ona se u svemu započinje kao opisana loptasta kupola, koja se slaže samo do visine tjemena čeonih lukova i na toj visini završava, tako da ostaje otvor omeđen kružnicom upisanom u tlocrtni kvadrat.
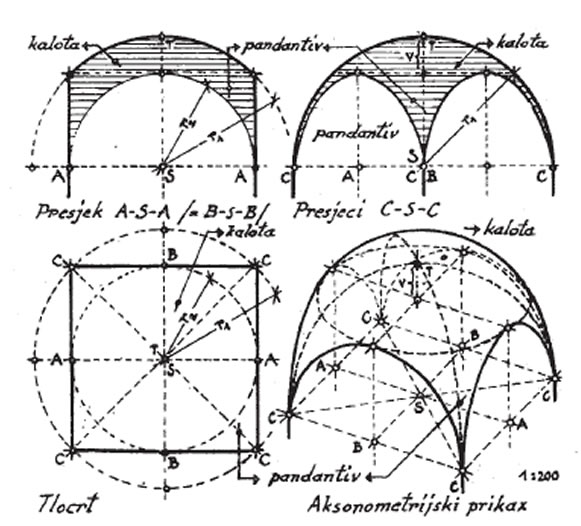
slika 5. Kupola nad prostorima kvadratičnog tlocrtnog oblika
Izrađena četiri dijela loptaste kupole do visine tjemenih točaka čeonih lukova predstavljaju četiri sferna trokuta, koji se nazivaju pandantivi. Na kružnim rubovima pandantiva nastavlja se zidanje pravilne polukružne kupole. Ta kupola, zajedno s pandantivima, naziva se bizantska kupola (sl. 6).
Arhitektura renesanse dodala je povrh pandantiva već spomenuti tambur s polukružnom kupolom povrh njega. Cesto se i ta kupola završavala manjim tamburom (za osvjetljenje i zračenje) s manjom kupolom, a taj se završetak naziva laterna (sl. 1).
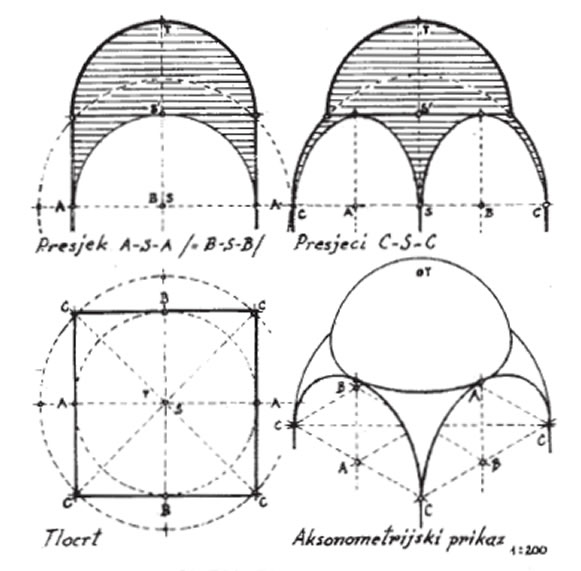
slika 6. Bizantska kupola
Češke kape
Češke su kape zapravo svodovi ili kalote polukružnih kupola. Grafički se konstruiraju tako da se iz kružnice opisane oko tlocrtnog kvadrata odredi tjeme i uporišne tačke čeonih lukova. Zatim se prema tim podacima odredi visina tjemena kupole i polumjer druge opisane kružnice izvan tlocrtnog kvadrata i to je tlocrtna kontura kupole horizontalno presječene kroz njezino središte (sl. 7.).
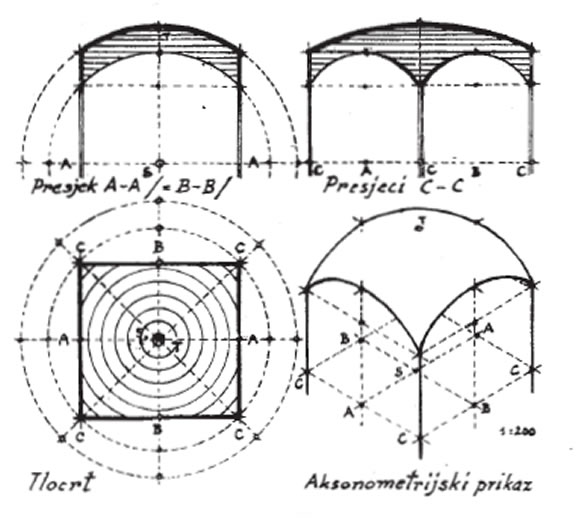
slika 7. Češka kapa
Češka se kapa može konstruirati i s većim promjerom kupole nego je onaj koji je u naprijed navedenom primjeru dobiven podatkom o kružnici opisanoj oko tlocrtnog kvadrata.
Može se konstruirati i nad pravokutnim (paralelogramskim) tlocrtima pazeći da strijela segmenta na najvećem razmaku (povrh dijagonale) ne bude manja od 1/6 do 1/8 toga razmaka. Iz tog se podatka grafički ustanovljuje polumjer kupole i ostali potrebni podaci (sl. 8).
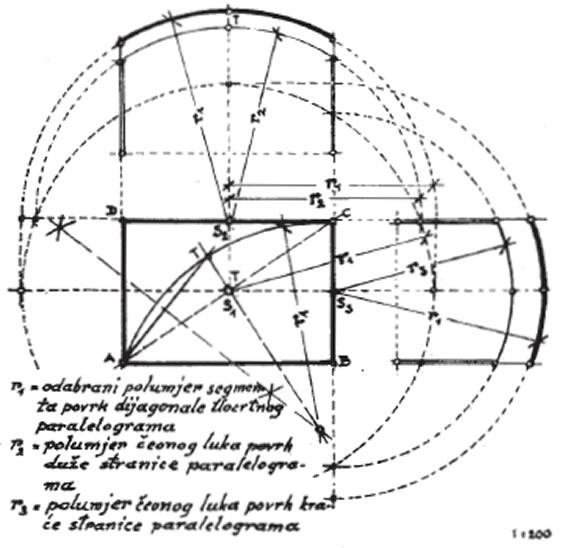
slika 8. Deskriptivno-geometrijska konstrukcija češke kape nad prostorom paralelogramskog tlocrtnog oblika
Izvor: Članak je preuzet iz knjige "Konstruktivni elementi zgrada", autora Đure Peulića i objavljena je u suradnji s knjižarom UPI2M BOOKS. Više informacija o knjizi možete dobiti putem niže navedenih kontakata.